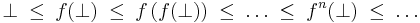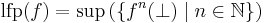Kleene fixed-point theorem

In the mathematical areas of order and lattice theory, the Kleene fixed-point theorem, named after American mathematician Stephen Cole Kleene, states the following:

Let L be a complete partial order, and let f : L → L be a continuous (and therefore monotone) function. Then the least fixed point of f is the supremum of the ascending Kleene chain of f.

It is often attributed to Alfred Tarski, but the original statement of Tarski's fixed point theorem is about monotone functions on complete lattices.

The ascending Kleene chain of f is the chain

$\bot \; \le \; f(\bot) \; \le \; f\left(f(\bot)\right) \; \le \; \dots \; \le \; f^n(\bot) \; \le \; \dots$

obtained by iterating f on the least element ⊥ of L. Expressed in a formula, the theorem states that

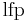$\textrm{lfp}(f) = \sup \left(\left\{f^n(\bot) \mid n\in\mathbb{N}\right\}\right)$

where $\textrm{lfp}$ denotes the least fixed point.

Kleene fixed-point theorem

See also